Throughout the ages, a spiral has represented infinite expansion, symbolizing the expansion of nature and the universe, reflecting the magical interconnectedness of our micro and macro cosmos. For centuries this knowledge was considered sacred, a way of understanding the deeper beauty and spirituality of life.
What is the Fibonacci of 1?
| F0 = 0 | F10 = 55 |
|---|---|
| F1 = 1 | F11 = 89 |
| F2 = 1 | F12 = 144 |
| F3 = 2 | F13 = 233 |
| F4 = 3 | F14 = 377 |
Comment see calculate le nombre d’or ? Le nombre d’or en géométrie “Le nombre d’or est le nombre réel positiv, noté Ï, égal à la fraction a/b si a et b sont deux nombres en proportion d’extrême et de moyenne raison. Read also : What is the biggest wave ever surfed?.” Here is the corresponding formula: Ï = (1 â5) / 2.
Quel est le 15e terme de la suite de Fibonacci ?
Read the first 15 terms of the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610. See the article : How can I use my X2 as a webcam?.
Comment s’écrit la suite de Fibonacci ?
La suite (Fn) de Leonardo Fibonacci is defined by F0 = 0, F1 = 1 et Fn = Fn â 1 Fn â 2 pour n > 1. Ses premiers termes sont donc F0 = 0, F1 = 1, F2 = 1, F3 = 2, F4 = 3, F5 = 5, F6 = 8, F7 = 13, F8 = 21, F9 = 34, F10 = 55, F11 = 89, F12 = 144, …
Quelle est la suite de Fibonacci ?
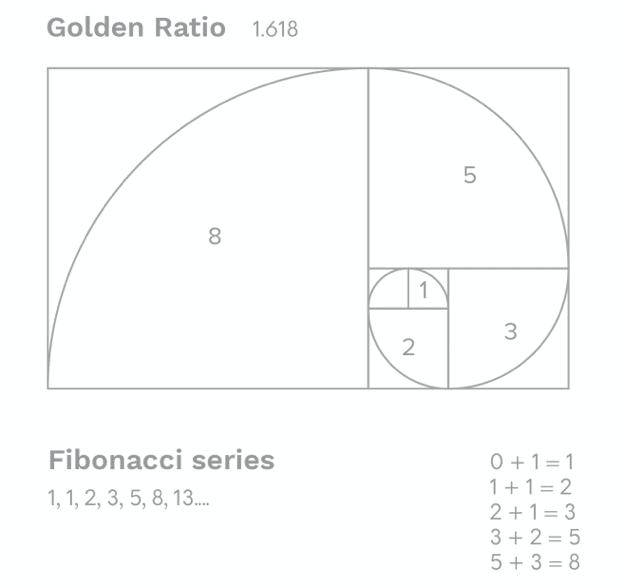
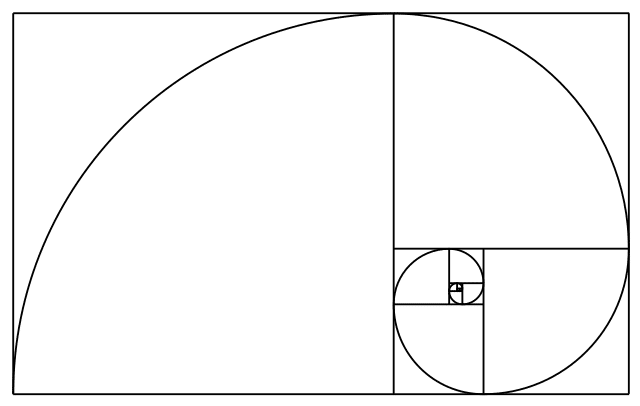
En mathématiques, la suite de Fibonacci est une suite de nombres entiers whose each successive term represents the sum of the two previous terms, et qui commence par 0 puis 1. Ainsi, les ten premiers qui la composent sont 0, 2, 1. , 3, 5, 8, 13, 21 and 34.
What is Fibonacci example?

Fibonacci number series: 0, 1, 1, 2, 3, 5, 8, 13,21,34,55,89,144,233, 377, 610, 987, 1597, 2584, 4181, 6765, 109416, 17616, 17616, 17616, 17616 75025, 121393, 196418, 317811, ⦠This may interest you : What are the 5 types of media?.
What are the first 10 Fibonacci numbers? The first 20 Fibonacci numbers are: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181.
What are 3 examples of ways Fibonacci numbers?
Here are some examples.
- Flower petals. The number of petals in a flower consistently follows the Fibonacci sequence. …
- Frog heads. The head of a flower is also subject to Fibonacci processes. …
- Pine cones. …
- 4. Fruits and vegetables. …
- Tree branches. …
- Shells. …
- Spiral galaxies. …
- Hurricanes.
What is Fibonacci sequence and give examples at least 5 of the Fibonacci sequence in nature?
4 flowers, fruit and leaves. On many plants, the number of petals is a Fibonacci number: buttercups have 5 petals; lilies and irises have 3 petals; some delphiniums have 8; corn marigolds have 13 petals; some asters have 21, while daisies can be found with 34, 55 or even 89 petals.
Which 3 things did the Fibonacci sequence lead to?
The mathematical ideas the Fibonacci sequence leads to, such as the golden ratio, spirals and self-similar curves, have long been appreciated for their charm and beauty, but no one can really explain why they resonate so clearly in the world of art and nature. The story began in Pisa, Italy in the year 1202.
What is the purpose of Fibonacci?
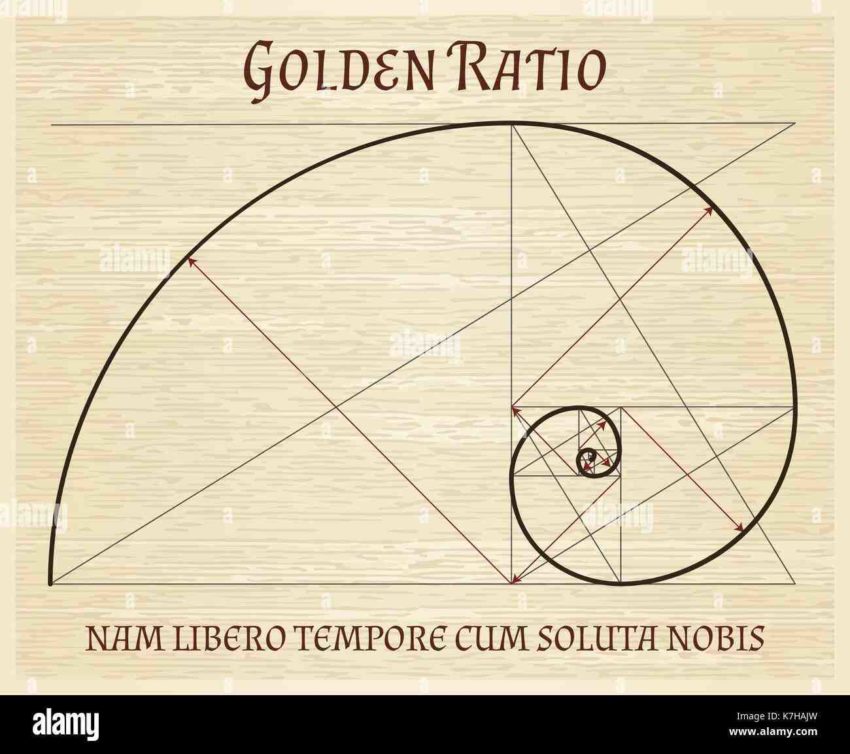
The golden ratio of 1.618 is derived from the Fibonacci sequence. Many things in nature have dimensional properties that adhere to the golden ratio of 1.618. The Fibonacci sequence can be applied to finance using four techniques including retracements, arcs, fans and time zones.
Why is the Fibonacci sequence so important?
Fibonacci Sequence Rule The golden ratio of 1.618, important to mathematicians, scientists and naturalists for centuries, is derived from the Fibonacci sequence. The quotient between each consecutive pair of Fibonacci numbers in the sequence approximates 1.618 or its inverse 0.618.
Why is the Fibonacci sequence in nature?
In nature, the growth and self-renewal of cell populations leads to the generation of hierarchical patterns in tissues, similar to the pattern of population growth in rabbits, which is explained by the classical Fibonacci sequence.
Why is Fibonacci important?
Fibonacci is remembered for two important contributions to Western mathematics: He helped spread the use of Hindu systems of writing numbers in Europe (0,1,2,3,4,5 instead of Roman numerals). The seemingly insignificant series of numbers later named the Fibonacci sequence after him.
Why is the Fibonacci sequence in nature? In nature, the growth and self-renewal of cell populations leads to the generation of hierarchical patterns in tissues, similar to the pattern of population growth in rabbits, which is explained by the classical Fibonacci sequence.
Why is Fibonacci sequence is so important?
Fibonacci Sequence Rule The golden ratio of 1.618, important to mathematicians, scientists and naturalists for centuries, is derived from the Fibonacci sequence. The quotient between each consecutive pair of Fibonacci numbers in the sequence approximates 1.618 or its inverse 0.618.
How is Fibonacci numbers used in real life?
Petals The number of petals in a flower consistently follows the Fibonacci sequence. Famous examples include the lily, which has three petals, buttercups, which have five (pictured left), chicory’s 21, daisies’ 34, and so on.
Why is the golden ratio so important?
04. Images: Golden Ratio (or Rule of Thirds) Composition is important to any image, whether it is to convey important information or to create an aesthetically pleasing photograph. The golden ratio can help create a composition that will draw the eye to the important elements of the image.
Why is Fibonacci golden ratio?

How is the golden ratio used in everyday life? This ideal ratio is used by many because of its apparent lure to the human eye. The golden ratio has been said to be the most appealing ratio, and is therefore often used. Everything from commercial advertising firms to painters, to even doctors, incorporate this ‘magical’ relationship into their work.
What are some examples in nature of the golden ratio list at least 5?
More examples of the golden ratio in nature:
- Frog heads. …
- Pineapple, Romanesco broccoli and cauliflower. …
- Pine cones. …
- Tree branches. …
- The eye, fins and tail fall off at golden section sections.
- Animal flight patterns. …
- Spiral galaxies.
What is the golden ratio of 5?
The rectangle above shows us a simple formula for the golden ratio. The square root of 5 is approximately 2.236068, so the golden ratio is approximately 0.5 2.236068/2 = 1.618034.
What are the 4 applications of golden ratio?
The Golden Ratio is a mathematical ratio you can find almost everywhere, such as nature, architecture, painting and music. When used specifically for design, it creates an organic, balanced and aesthetically pleasing composition.
What are Fibonacci ratios?
What is the Fibonacci ratio? The Fibonacci ratios are derived from the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, and so on. Here, each number is equal to the sum of the previous two numbers. Fibonacci ratios are based on mathematical relationships found in this formula.
What are the strongest Fibonacci numbers? Fibonacci retracements are ratios used to identify potential reversal levels. These ratios are found in the Fibonacci sequence. The most popular Fibonacci retracements are 61.8% and 38.2%. Note that 38.2% is often rounded to 38% and 61.8 is rounded to 62%.
What is Fibonacci golden ratio?
The important part is that as the numbers get larger, the quotient between each consecutive pair of Fibonacci numbers approximates 1.618, or its inverse 0.618. This proportion is known by many names: the golden ratio, the golden mean, Ï and the divine proportion, among others.
What is the Golden Ratio in nature?
The golden ratio is 1.618, represented by the Greek letter ‘phi’, said to be a mathematical connection between two aspects of an object. Also called the Fibonacci sequence, it can be found throughout nature: plants, animals, weather patterns, star systems – it is always present in the universe.
What is the Golden Ratio in simple terms?
The golden ratio or golden mean, represented by the Greek letter phi (Ï), is an irrational number roughly equal to 1.618. The golden ratio occurs when the ratio of two numbers is the same as the ratio of their sum to the larger of the two numbers.
What do the Fibonacci levels mean?
In finance, Fibonacci retracement is a method of technical analysis for determining support and resistance levels. It is named after the Fibonacci series, the ratio of which provides price levels to which markets tend to retrace part of a move before a trend continues in the original direction.
How do you trade Fibonacci levels?
Fibonacci levels used in the financial markets. The ratio of 38.2% is derived by dividing a number in the Fibonacci series by the number two to the right. For example: 89/233 = 0.3819. The ratio of 23.6% is derived by dividing a number in the Fibonacci series by the number three places to the right.
Which Fibonacci levels are best?
What are the best Fibonacci Retracement settings? The most commonly used Fibonacci retracement levels are at 23.6%, 38.2%, 61.8% and 78.6%.